2024. 12. 13. 22:03ㆍlearning more/이산수학
학습 목표
- 명제와 명제가 아닌 것을 구분
- 다양한 논리연산의 기능을 이해
- 합성명제의 진리값 구하기
- 한정자가 포함된 술어논리 구사
명제
정의 : 참과 거짓을 구별할 수 있는 문장이나 수학적 식을 명제라고 한다.
> 명제의 진리값 (truth value)
- 참 True T : 명제가 타다한 경우
- 거짓 False, F : 명제가 타당하지 않은 경우
명제의 종류
- 합성명제
- 조건명제, 쌍조건명제
- 항진명제, 모순명제
예제) 명제인지 아닌지 구분
- 6은 2의 배수다 - 참, 명제
- 철수는 공부를 잘 한다 - 명제가 아님, 기준에 따라 다름
- 제트기는 빠르다 - 명제가 아님, 기준에 따라 다름
- 2 + 3 = 7, 명제, 거짓
- x + 2 = 0, 명제가 아님, x 값에 따라 참과 거짓이 달라짐
- 하루는 25시간 이다 . 명제, 거짓
- 웃으며 삽시다 - 단순한 의견(권유문), 명제가 아님
예제) 명제의 진리값
- 2, 3, 6은 소수이다 - 거짓, 6은 소수가 아니다.
- 소수의 개수는 무한하다 - 참
- 128 = 2의 6승 - 거짓, 2의 6승은 64
- 프랑스의 수도는 파리이다 - 참
논리연산
참, 거짓을 구별할 수 있는 명제를 대상으로 하는 연산이다. 우리가 실수 집합에서 사칙연산이라고 하면 실수와 실수의 덧셈, 뺄셈, 곱셈, 나눗셈 등을 말하는 것처럼, 논리 연산은 명제들의 집한에 대해 고안해 낸 연산이다.
대표적인 논리연산
- 논리곱
- 논리합
- 부정
- 배타적 논리합
논리연산도 기호로 나타나며 이 기호를 "논리연산자"라고 부름.
 |
 |
- 부정 (Negation)
- 기호: ¬ 또는 ~
- 의미: 주어진 명제의 진리값을 반전시킵니다.
- 예시: ¬p는 "p가 아니다"를 의미하며, p가 참이면 ¬p는 거짓이 되고, p가 거짓이면 ¬p는 참이 됩니다.
- 논리곱 (Conjunction)
- 기호: ∧
- 의미: 두 명제가 모두 참일 때만 참이 되는 연산입니다.
- 예시: p ∧ q는 "p 그리고 q"를 의미하며, p와 q가 모두 참일 때만 참입니다.
- 논리합 (Disjunction)
- 기호: ∨
- 의미: 두 명제 중 하나 이상이 참이면 참이 되는 연산입니다.
- 예시: p ∨ q는 "p 또는 q"를 의미하며, p나 q 중 하나라도 참이면 참입니다.
- 배타적 논리합 (Exclusive OR)
- 기호: ⊕
- 의미: 두 명제 중 정확히 하나만 참일 때 참이 되는 연산입니다.
- 예시: p ⊕ q는 "p 또는 q지만 둘 다 동시에 참일 수는 없다"를 의미합니다.
- 조건문 (Implication)
- 기호: →
- 의미: 첫 번째 명제가 참이고 두 번째 명제가 거짓일 때만 거짓이 되는 연산입니다.
- 예시: p → q는 "p이면 q이다"를 의미하며, p가 참이고 q가 거짓일 때만 거짓입니다.
- 쌍방 조건문 (Biconditional)
- 기호: ↔
- 의미: 두 명제가 모두 같을 때(둘 다 참이거나 둘 다 거짓일 때) 참이 되는 연산입니다.
- 예시: p ↔ q는 "p이면 q이고, q이면 p이다"를 의미합니다
논리합
(1) 명제
- p: 3 > 1
- q: 4 > 8
논리합: p∨q
진리값
- p: 참 (3 > 1은 참입니다)
- q: 거짓 (4 > 8은 거짓입니다)
논리합의 진리값
- p∨q: 참
- p가 참이기 때문에, q의 값에 관계없이 전체 논리합은 참입니다.
(2) 명제
- p: 2 × 3 = 8
- q: 4 - 2 = 3
- : 소크라테스는 살아 있다.
논리합: p∨q∨r
진리값
- p: 거짓 (2 × 3 = 6, 따라서 거짓입니다)
- : 거짓 (4 - 2 = 2, 따라서 거짓입니다)
- r: 거짓 (소크라테스는 역사적으로 사망한 인물입니다)
논리합의 진리값
- p∨q∨r: 거짓
- 모든 개별 명제가 거짓이므로, 전체 논리합도 거짓입니다.
논리곱 작성
- (1) 명제
- p: 홀수와 홀수를 더하면 짝수이다.
- q: 짝수와 홀수를 곱하면 짝수이다.
- 논리곱: p∧q
- (2) 명제
- p: 키보드는 입력장치이다.
- q: USB는 메모리이다.
- r: 모니터는 기억장치이다.
- 논리곱: p∧q∧r
진리표 작성
(1) p∧q 진리표
| p | q | p∧q |
| 참 | 참 | 참 |
| 참 | 거짓 | 거짓 |
| 거짓 | 참 | 거짓 |
| 거짓 | 거짓 | 거짓 |
- 두 명제 모두 참일 때만 전체가 참입니다.
- 2개다 참이므로 답은 참
(2) p∧q∧r 진리표
| p | q | r | p∧q∧r |
| 참 | 참 | 참 | 참 |
| 참 | 참 | 거짓 | 거짓 |
| 참 | 거짓 | 참 | 거짓 |
| 참 | 거짓 | 거짓 | 거짓 |
| 거짓 | 참 | 참 | 거짓 |
| 거짓 | 참 | 거짓 | 거짓 |
| 거짓 | 거짓 | 참 | 거짓 |
| 거짓 | 거짓 | 거짓 | 거짓 |
- 세 명제 모두 참일 때만 전체가 참입니다.
- r이 거짓이므로 답은 거짓
부정(¬) 진리표
| p | ¬p |
| 참 (True) | 거짓 (False) |
| 거짓 (False) | 참 (True) |
- 부정 연산은 명제 p의 진리값을 반전시킵니다.
- 가 참이면 ¬p는 거짓.
- p가 거짓이면 ¬는 참.
배타적 논리합(⊕) 진리표
| p | q | p⊕q |
| 참 (True) | 참 (True) | 거짓 (False) |
| 참 (True) | 거짓 (False) | 참 (True) |
| 거짓 (False) | 참 (True) | 참 (True) |
| 거짓 (False) | 거짓 (False) | 거짓 (False) |
- 배타적 논리합(Exclusive OR, XOR)은 두 명제 중 정확히 하나만 참일 때 결과가 참이 됩니다.
- 와 q가 모두 같으면 결과는 거짓.
- p≠q(서로 다르면), 결과는 참.
조건명제
명제 p와 q가 있을 때, 명제 p가 조건의 역할을 수행하고 명제 q가 결론의 역할을 수행하는 경우
조건 명제의 구성
- 형태: p→q
- 여기서 p는 전건(Antecedent) 또는 가정(Condition)이고, q는 후건(Consequent) 또는 결론(Consequence)입니다.
- "만약 p이면 이다"라고 읽습니다.
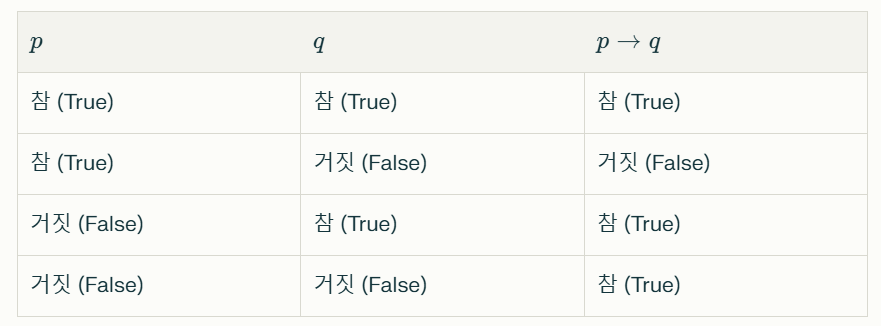
- 가 참이고 q가 거짓인 경우에만 전체 명제가 거짓이 됩니다.
- 나머지 경우에는 모두 참입니다.
- 수학적 예시:
- p: "2는 짝수이다."
- q: "2는 소수이다."
- 조건 명제: "만약 2가 짝수라면, 2는 소수이다." 이 경우, 전건과 후건 모두 참이므로 전체 명제는 참입니다.
- 일상적 예시:
- p: "비가 온다."
- q: "우산을 쓴다."
- 조건 명제: "만약 비가 오면, 우산을 쓴다." 이 경우, 비가 오지 않으면 우산을 쓰지 않아도 되므로 전건이 거짓일 때 전체 명제는 자동으로 참입니다.
쌍조건 명제
두 명제가 서로 논리적으로 동등한지를 나타내는 명제로, "p이면 q이고, q이면 p이다"라는 형태로 표현됩니다. 이는 두 명제가 동시에 참이거나 동시에 거짓일 때 참이 되는 논리 연산입니다. 쌍조건 명제는 논리적 동치성을 나타내며, 수학적 증명이나 논리적 추론에서 자주 사용됩니다.
쌍조건 명제의 구성
- 형태: p↔q
- 여기서 p와 q는 각각의 명제입니다.
- "p이면 q이고, q이면 p이다" 또는 "p와 q는 서로 동치이다"라고 읽습니다.
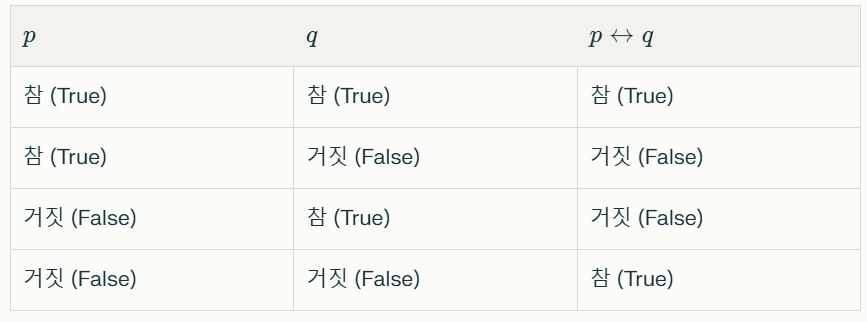
- 두 명제가 모두 참이거나 모두 거짓일 때 전체 명제가 참입니다.
- 두 명제의 진리값이 다를 때 전체 명제가 거짓입니다.
쌍조건 명제의 의미
- 동시 참일 때: 두 명제가 모두 참이면 쌍조건 명제는 참입니다.
- 동시 거짓일 때: 두 명제가 모두 거짓이어도 쌍조건 명제는 참입니다.
- 진리값이 다를 때: 한쪽이 참이고 다른 쪽이 거짓이면 쌍조건 명제는 거짓입니다.
예시
- 수학적 예시:
- p: "정수 n은 짝수이다."
- q: "정수 n은 2로 나누어떨어진다."
- 쌍조건 명제: "정수 n이 짝수이면, n은 2로 나누어떨어지고, 정수 n이 2로 나누어떨어지면 n은 짝수이다." 이 경우, 두 조건은 서로 동치이므로 전체 명제는 항상 참입니다.
- 일상적 예시:
- p: "오늘은 토요일이다."
- q: "내일은 일요일이다."
- 쌍조건 명제: "오늘이 토요일이면 내일은 일요일이고, 내일이 일요일이면 오늘은 토요일이다." 이 경우, 두 조건이 동시 성립할 때만 전체가 참입니다.
논리적 동치
논리적 동치는 두 명제가 항상 동일한 진리값(True/False)을 가지는 경우를 의미합니다. 즉, 어떤 상황에서도 두 명제의 결과가 같다면, 이 두 명제는 논리적으로 동치라고 합니다. 논리적 동치는 기호로 p≡q 또는 p↔q 로 표현됩니다
역, 이, 대우
논리학에서 명제의 변형 중 "역", "이", "대우"는 주어진 조건 명제를 변형하여 새로운 명제를 만드는 방법
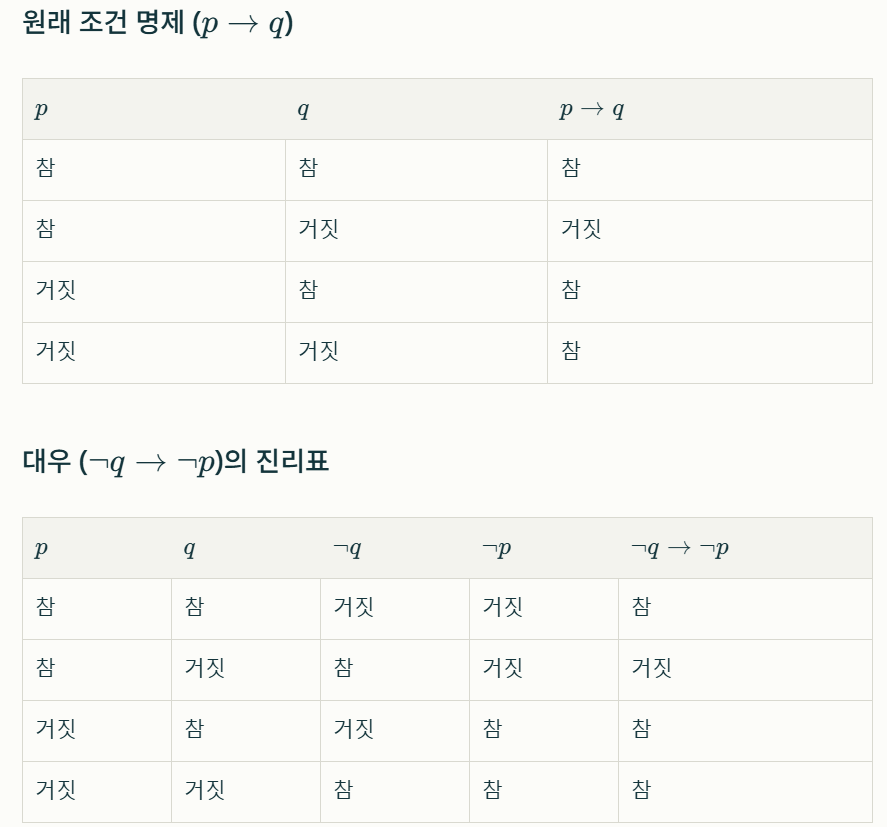
- 역과 이는 원래 조건 명제와 진리값이 다를 수 있으므로 주의해서 사용해야 합니다.
- 대우는 원래 조건 명제와 항상 같은 진리값을 가지므로 논리적 증명에서 유용하게 사용됩니다.
항진명제와 모순명제
항상 참인 명제 항진명제 / 항상 거진인 명제를 모순명제
술어논리와 명제함수
명제논리 - 명제
술어논리 - 명제함수
- 변수의 값에 의해 함수의 진리값이 결정되는 문장이나
전체한정자 (universal quantifier, ∀)
- 전체한정자는 “모든” 또는 “임의의”를 의미하며, 명제함수 ∀𝒙𝑷(𝒙)와 같이 사용되었을 경우에는 정의역의 모든 [임의의] 𝒙에 대해서 𝑷(𝒙)가 참(T)임을 의미한다.
존재한정자 (existential quantifier, ∃)
- 존재한정자는 “존재한다”를 의미하며, 명제함수 ∃𝒙𝑷(𝒙)와 같이 사용되었을 때는 정의역의 어떤 𝒙에 대해서 𝑷(𝒙)가 참(T)임을 의미한다